vue计算方式
力学计算大全力学试验中常用公式
(一)：振动台正弦推力的计算
振动台工作时，振动所需要输出的力主要为下：
$$ F = (m_0 +m_1 + m_2 + ...)A $$
式中，\(F\)为推力\(N\)
\(m_0\):振动台运动部分有效质量(扩展台面、水平滑台、动圈、连接件等)\(kg\);
\(m_1\):夹具（连接产品和振动台）质量 \(kg\);
\(m_2\):产品质量 \(kg\);
\(A\):试验加速度 \(m/s²\)。一般情况下用工程单位\(g\)，\(1g＝9.8m/s^2\)
振动试验中，假设：
1.振动台运动部分（一般包括动圈、连接板簧、连接件）等质量为\(500kg\)
2.试件质量为\(1000kg\)
3.夹具质量\(500kg\)
4.试验量级\(10m/s^2\)
则推力\(F\)为：\((500+1000+500)×10=20000N\)
(二)：正弦振动时速度、位移、加速度的换算
式中，A 为试验加速度 (m/s²)；V 为试验速度(m/s)；ω=2πf（角速度），f 为试验频率 (Hz)。
式中，V 和ω 与上式同义，D 为位移(mm0-p)单峰值.
式中，A、D 与以上同义，该公式亦可简化为：
式中，A 的单位为g，1g=9.8m/s²
(三):加速度、位移、速度平滑交越点频率的计算公式
- 加速度与速度平滑交越点频率的计算公式：
$$ f_{A-V} =\frac{A}{6.28×V} $$
\(A\):加速度 \( g \).
\(V\):速度 \( m/s \) - 速度与位移平滑交越点频率的计算公式：
$$ f_{V-D} =\frac{V×10^3}{6.28×D} $$
\(D\):位移 \( g \).
\(V\):速度\( m/s \) - 加速度与位移平滑交越点频率的计算公式：
$$ f_{A-D} =\sqrt{\frac{A×10^3}{{(2\pi)}^2×D}} $$
\(A\):加速度 \( g \).
\(D\):位移 \( mm \)
(四):随机分辨率计算公式
$$ \Delta{f}=\frac{f_{max}}{N} $$式中：
\(\Delta{f}\)：频率分辨率\({HZ}\)
\(f_{max}\)：最高控制频率
\({N}\)：为谱线数
\(f_{max}\)是\(\Delta{f}的整数倍\)
(五):随机振动加速度总均方根值得计算公式
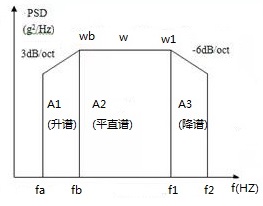
平直谱计算公式：
$$A_2=w\Delta{f}=w(f_1-f_b)$$升谱计算公式：
$$ A_1 = \int_{f_a}^{f_b}w(f)df = \frac{w_bf_b}{m+1}[1-(\frac{f_a}{f_b})^{m+1}]$$降谱计算公式:
$$ A_3 = \int_{f_1}^{f_2}w(f)df = \frac{w_1f_1}{m-1}[1-(\frac{f_1}{f_2})^{m-1}]$$上式中，\(m=N/3\),\(N\)为谱线的斜率\(dB/octive\)
由升谱、平直谱、降谱得到加速度的总均方根值：
$$G_{rms} = \sqrt{A_1+A_2+A_3}$$(六):dB与百分比的转换
(七)正弦振动力学条件设置
| 序号 | 频率(Hz) | 位移(o-p) | 速度(m/s) | 加速度(g) |
|---|---|---|---|---|
| 好的顶顶顶 | ||||